large effects

Much of statistical practice is concerned with distinguishing signal from noise. For example, significance tests quantify the likelihood that observations could be explained by noise alone.

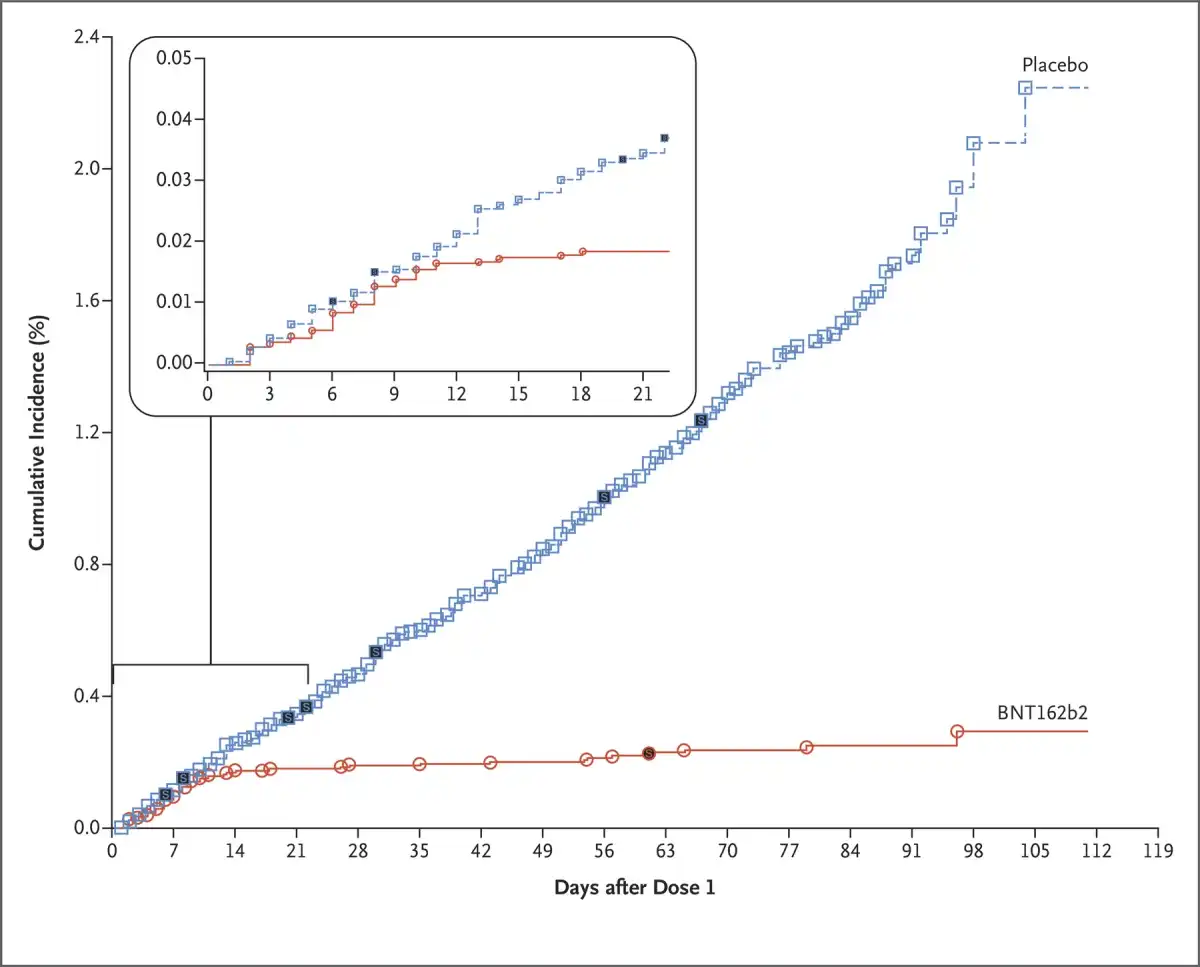
But when something really works, it shouldn't be hard to distinguish the effect from noise. For example, this chart from the phase III study of Pfizer's Covid-19 vaccine shows cumulative cases in the control (blue) and treatment (red) groups:

You don't need fancy statistics to see that the vaccine works.

Similarly, you don't need much cleverness to distinguish the survival probability of skydiving with a parachute versus without one.

If I'm in a situation where I do need statistical methods to decide whether an intervention has a real effect, I tend to ask myself whether I could be spending my time on something more impactful.

This is one reason I don't see classical statistics as first-order important to AI research. Sure, reasoning under uncertainty is important, but the high-order bits are (almost by definition) the things we're not particularly uncertain about. Pre deep learning, image classification was a hard problem for decades even for datasets with no intrinsic uncertainty (where the Bayes error rate is zero). The solution was better representations, not more rigorous quantification of uncertainty.

Caveats: sometimes it is important to quantify effects near the noise level, because:

• There is a lot of noise, so that even a large effect might not be apparent.You'd expect this in studying the effectiveness of antidepressant drugs, for example, since psychology is complicated and influenced by a wide range of hard-to-control-for factors.
• Data is extremely scarce or expensive. (largely equivalent to the previous case, since noise decreases as $\sqrt{n}$).
• Combining interventions can have large impact even if their individual effects are small. For example, repeated iterations of A/B testing might improve a web site by quite a bit even if none of the changes had large effects individually; it only matters that each tweak has some independent positive effect.
• The effect is not from an intervention, but a from a phenomenon of interest for its own sake. For example, detecting exoplanets is of scientific interest even (especially) because they're difficult to observe.