infinitesimal

The Leibniz calculus notation using infinitestimal quantities like $dx$ or $dt$ is simultaneously

1. Very sensible and intuitive, but also
2. Constantly confusing to me.

A lot of this is probably specific to my own idiosyncratic understanding, but in any case this note is an attempt to work through points that have confused me.

Discrete time. I like that infinitesimals connect intuitively to the finite-sum case where we're summing over some change $\Delta x$ at each timestep. But when considering discrete 'timesteps' we often implicitly take $\Delta t = 1$, which can make it ambiguous which of $\Delta x$ and $\frac{\Delta x}{\Delta t}$ we actually mean. In general, if a change is 'per timestep', it should be written as $\frac{\Delta x}{\Delta t}$ (or similar) to emphasize that two timesteps would give twice as much change, half a timestep half as much, etc.

Dependence. if $x(t)$ is a function of time, then its derivative $\frac{dx}{dt}$ is also a function of time. But what about $dx$ and $dt$ individually? Are these also functions of time? If so, should we not write them with this explicit dependence?

Let's start with $dt$. Ultimately we can think of whatever derivative or integral we're evaluating as the limit of a ratio or sum as some 'width' variable $\epsilon$ goes to zero. In principle we could define $dt(\epsilon, t)$ as nonuniform in $t$, describing e.g. a sum in which the 'width' of the time buckets is larger in some parts of the domain than in others. But usually it makes sense to identify $\epsilon$ with $dt$, i.e., consider the limit of all timesteps becoming infinitesimally small in a uniform way, and then $dt$ has no time dependence.

On the other hand, $x(t)$ is a function of time, and any small change in time $dt$ will induce a corresponding change $dx(t) = x(t + dt) - x(t)$. This quantity $dx(t)$ is absolutely a function of time. It is also, implicitly, a function of $dt$, in that a larger input change $dt$ will lead to larger output change $dx$, but more properly we can think of both of these as being some function of the underlying $\epsilon$.

Partial differentials. How do $dx$ and $\partial x$ relate to each other? Do they have the same units? Does $dx - \partial x = 0$, does $\frac{d x}{\partial x} = 1$, or is there a clear principle for why neither of these can occur in a valid expression?

I think this starts to implicate a computational graph view of calculus. For concreteness of illustration, let $x = t^2$, and consider some function $f(x, t)$. The full picture here looks like 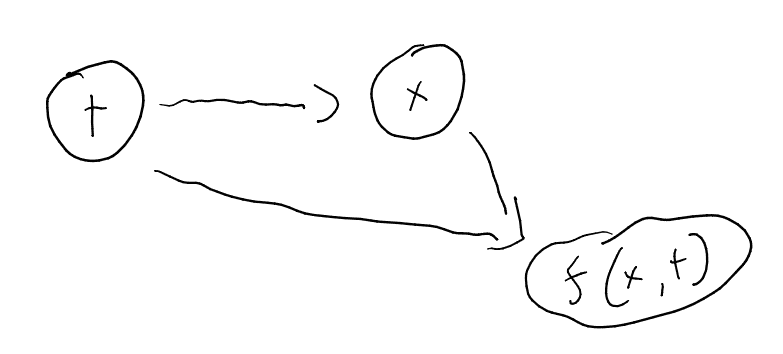in which everything is downstream of $t$, which functions as an exogenous or 'input' variable. In this picture, the total derivative $\frac{df}{dt}$ is a question about the graph as a whole: how will the value at the output node $f$ change in response to a change at the input node $t$? The partial derivative $\frac{\partial f}{\partial t}$ is a local question about the final node: how will the value $f(x, t)$ of that node change if we vary the second argument while holding the first argument constant? We can relate these using the law of total differentiation:

This is in terms of ratios of infinitesimals, where a $\partial$ is always in a ratio with another $\partial$ (and similarly for $d$) so the 'units' always cancel out. In general it's not valid to cancel across infinitesimal units, e.g. we can't simplify $\frac{\partial f}{\partial x} \frac{dx}{dt} = \frac{\partial f}{dt}$ and it's not clear what it would mean if we could.

I think the right way to think about this is that global/total differentials can generally be treated within a single global limit: for some perturbation $\Delta t$ to the input of the computation graph, the perturbations $\Delta x$ and $\Delta f$ fall out naturally, so there is a consistent process relating all of these quantities, in some sense a single coherent thought experiment, which allows us to meaningfully ask about their ratios.

By contrast, the partial derivative $\frac{\partial f}{\partial t}$ is asking about a modified copy of the graph where we freeze all inputs to $f$ except for $t$.This is vaguely reminiscent to the graph surgery prescribed by do-calculus for causal inference, but only vaguely. In this graph, $\delta f$ and $\delta t$ are the only changes that are even defined; the $\delta$ indicates units corresponding to this particular thought experiment, so the only way to 'leave the thought experiment' and get an objectively meaningful quantity is to consider the ratio $\frac{\partial f}{\partial t}$ or its inverse. There is no meaningful way for partial differentials to interact with quantities in a different thought experiment.

The view of total differentials as a single coherent thought experiment is complicated when we have multiple independent variables. Suppose we we had both $t$ and $r$ as exogenous inputs, took $x(r, t)$ as a function of both of them, and then asked about $dx/dt$? I guess derivatives wrt $t$ have to be interpreted in terms of a limiting process as $dt$ goes to zero. And separately if we're computing derivatives with respect to $r$, there is a limiting process as $dr$ goes to zero. But these are separate processes, not tied to any common rate. To put a point on it: what is $\frac{\Delta t}{\Delta r}$ in this experiment? It's not a well-defined quantity because neither $t$ nor $r$ is a function of the other; we have total freedom in the relative rate at which those differentials go to zero. So when we're asking about $\frac{\Delta x}{\Delta r}$ this must be a different $\Delta x$ from that in $\frac{\Delta x}{\Delta t}$: the first exists in a thought experiment where we've changed $r$ while leaving $t$ unchanged, and the second in an opposite thought experiment. TODO resolve this.

Differential operators. Why can we write $\frac{d}{dt}$ but not $\frac{dt}{d}$?

Higher-order derivatives. Why is the second derivative written as $\frac{d^2 x}{dt^2}$ and what do the individual terms of these mean?

It might help me to work through Wikipedia's description of differentials as linear maps. For a function $f(x)$, we define the differential $df = f' dx$. A multidimensional function $f(x, y)$ has differential

Here the differential is only defined on functions; we finesse this by treating $x$ and $y$ as functions on a 'standard infinitesimal' $p$, so that $x(p) = p$ and $y(p) = p$? I'm confused by the 'standard infinitesimal' setup because it seems like it implies a dependence between $x$ and $y$ that doesn't necessarily exist.