instrumental variables

The front-door adjustment allows identifying causal affects using a mediating variable that sits on the causal chain between X and Y. For smoking and lung cancer, the mediating variable could be tar in the lungs. What's important is that this mediating variable is not directly influenced by any confounders we're worried about, like genetic factors.

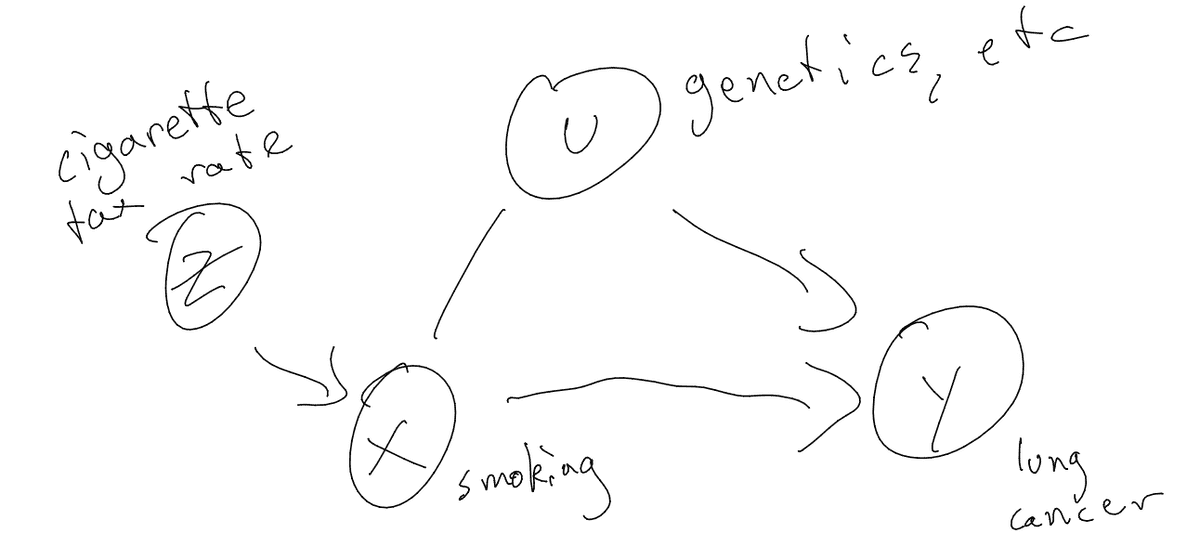
But we can also use an instrumental variable, which sits behind X on the causal chain. Like a mediating variable, it should not be affected by the confounders we're worried about. For example, we might use the tax rate on cigarette products. Higher taxes will presumably reduce the rate of smoking independently of any genetic factors. In that sense, they function like a soft intervention, a natural experiment.

The causal graph looks like:

An equivalent framing of this causal graph is as an 'treatment with imperfect compliance'. Our treatment (Z) doesn't fully determine what actually happens (X), and we need to correct for this.

Intuitively, if changing the tax rate causes lung cancer to change, it must (following the assumptions laid out by this graph) be through the causal path of smoking.

Quantitatively, if Z and X are tightly coupled, then $p(y | do(x))$ will be very similar to $p(y | do(z))$. If they are barely coupled, then we'll need a lot of data to get an estimate.

According to wikipedia, the average causal effect of smoking is only identifiable in the case of linear models. In general it is possible to derive bounds that can be estimated.