Modified: July 09, 2022
convex
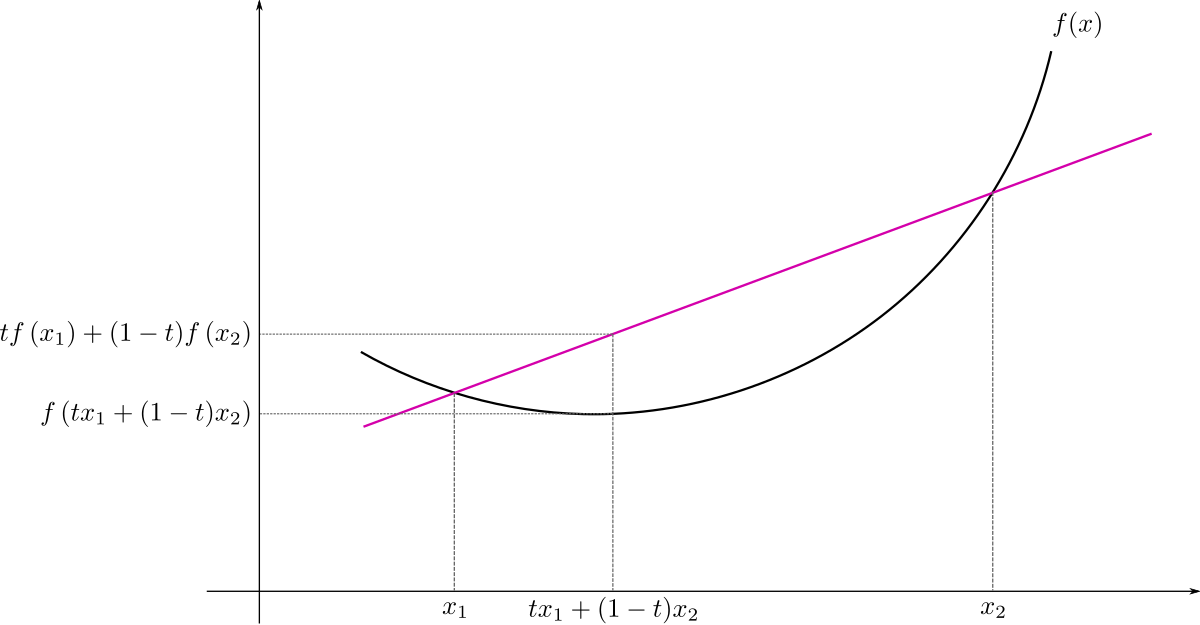
This page is from my personal notes, and has not been specifically reviewed for public consumption. It might be incomplete, wrong, outdated, or stupid. Caveat lector.A convex function satisfies the property that a line between any two points on its graph is on or above the graph:
for any . It is strictly convex if this inequality is strict. Wikipedia has this nice illustration of the definition:
A slight generalization of this definition, , is sometimes called Jensen's inequality.
The second derivative of a differentiable convex function must be nonnegative; that is, the derivative must be non-decreasing. In the multivariate setting, the Hessian of a differentiable convex function must be positive semidefinite.
A convex function is always greater than or equal to its first-order Taylor expansion. A function is -strongly convex if it exceeds its linear approximation by a quadratic quantity: . An equivalent condition is that is convex.